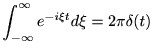問 1
畳み込みの定理、Wiener-Khintchineの定理を導出せよ。
畳み込みの定理、Wiener-Khintchineの定理を導出せよ。
証明 0.2
まず、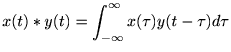 であるから
であるから
また、![$\displaystyle x[n]*y[n]=\sum_{m=-\infty}^{\infty}x[m]y[n-m] $](img14.png) であるから
であるから
さらに、
であるから、(証明は後述)
そして、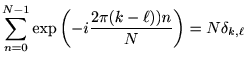 であるから、
であるから、
式(1)について。
ここで、
であるから、考えるべきは の項の部分のみ。
の項の部分のみ。
ここで、Riemann-Lebesgueの補助定理より、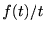 は原点以外では連続である
から、右辺の積分区間が
は原点以外では連続である
から、右辺の積分区間が
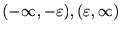 である項は零に収束する。
である項は零に収束する。
より、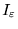 を不等式で評価すれば、
を不等式で評価すれば、
ここで、複素積分を実行すれば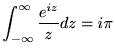 さらに、
さらに、
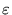 は任意の正数なので、
は任意の正数なので、
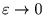 を考えれば、
を考えれば、
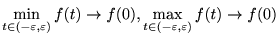 従って、
従って、
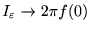 証明終了。
証明終了。
まず、
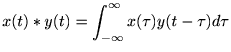
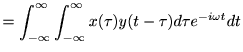 |
||
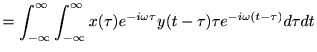 |
||
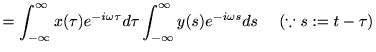 |
||
また、
![$\displaystyle x[n]*y[n]=\sum_{m=-\infty}^{\infty}x[m]y[n-m] $](img14.png)
![$\displaystyle =\sum_{n=0}^{N-1}\sum_{m=0}^{N-1}x[m]y[n-m]\exp \left(-i\frac{2\pi kn}{N}\right)$](img16.png) |
||
![$\displaystyle =\sum_{m=0}^{N-1}x[m]\exp\left(-i\frac{2\pi k m }{N}\right) \sum_{\ell=0}^{N-1}y[\ell ]\exp\left(-i\frac{2\pi k \ell}{N}\right) $](img17.png) |
||
さらに、
であるから、(証明は後述)
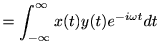 |
||
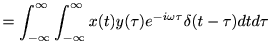 |
||
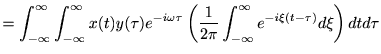 |
||
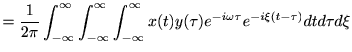 |
||
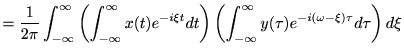 |
||
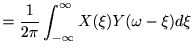 |
||
そして、
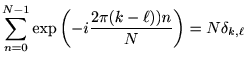
![$\displaystyle =\sum_{n=0}^{N-1} x[n]y[n]\exp\left(-i\frac{2\pi kn}{N}\right)$](img30.png) |
||
![$\displaystyle =\sum_{n=0}^{N-1} x[n]y[n]\exp\left(-i\frac{2\pi kn}{N}\right)$](img30.png) |
||
![$\displaystyle =\sum_{n=0,\ell=0}^{N-1} x[n]y[n]\exp\left(-i\frac{2\pi \ell n}{N}\right)\delta_{k,\ell}$](img31.png) |
||
![$\displaystyle =\sum_{n=0,\ell=0}^{N-1} x[n]y[n]\exp\left(-i\frac{2\pi\ell n}{N}... ...t(\frac{1}{N}\sum_{m=0}^{N-1}\exp\left(-i\frac{2\pi(k-\ell) m}{N}\right)\right)$](img32.png) |
||
![$\displaystyle =\sum_{n=0,\ell=0,m=0}^{N-1} x[n]y[n]\exp\left(-i\frac{2\pi\ell(n-m) }{N}\right) \frac{1}{N}\exp\left(-i\frac{2\pi k m}{N}\right)$](img33.png) |
||
![$\displaystyle =\sum_{n=0,m=0}^{N-1} x[n]y[n]\delta_{n,m}\exp\left(-i\frac{2\pi k m}{N}\right)$](img34.png) |
||
![$\displaystyle =\sum_{n=0,m=0}^{N-1} x[n]y[m]\delta_{n,m}\exp\left(-i\frac{2\pi k m}{N}\right)$](img35.png) |
||
![$\displaystyle =\sum_{n=0,\ell=0,m=0}^{N-1} x[n]y[m]\exp\left(-i\frac{2\pi\ell(n-m) }{N}\right) \frac{1}{N}\exp\left(-i\frac{2\pi k m}{N}\right)$](img36.png) |
||
![$\displaystyle =\frac{1}{N}\sum_{n=0,m=0,\ell=0}^{N-1} x[n]y[m]\exp\left(-i\frac{2\pi\ell n}{N}\right) \exp\left(-i\frac{2\pi (k-\ell)m}{N}\right)$](img37.png) |
||
![$\displaystyle =\frac{1}{N}\sum_{\ell=0}^{N-1} \left(\sum_{n=0}^{N-1}x[n]\exp\le... ...t) \left(\sum_{m=0}^{N-1}y[m]\exp\left(-i\frac{2\pi(k-\ell) m}{N}\right)\right)$](img38.png) |
||
![$\displaystyle =\frac{1}{N}\sum_{\ell=0}^{N-1}X[\ell]Y[k-\ell]$](img39.png) |
||
式(1)について。
示すべきは、任意のテスト関数![]() について、以下が成立することを示せばよ
い。
について、以下が成立することを示せばよ
い。
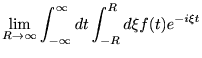 |
ここで、
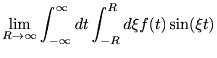 |
![$\displaystyle = \lim_{R\to\infty}\int_{-\infty}^\infty d t f(t)\left[ \frac{-\cos(\xi t)}{t} \right]_{-R}^{R}$](img45.png) |
|
![$\displaystyle = \lim_{R\to\infty}\int_{-\infty}^\infty d t f(t)\left[ \frac{-\cos(Rt)}{t}-\frac{-\cos(-Rt)}{t} \right]$](img46.png) |
||
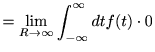 |
||
であるから、考えるべきは
そこで、
![]() の原点特異性より積分区間を
の原点特異性より積分区間を
![]() で区切って考えると、
で区切って考えると、
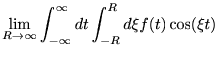 |
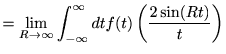 |
|
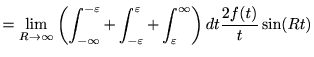 |
||
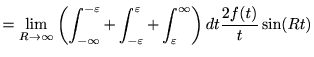 |
ここで、Riemann-Lebesgueの補助定理より、
よって、残りの項を考えると、
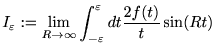 |
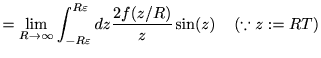 |
より、
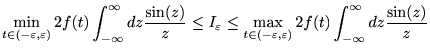 |
ここで、複素積分を実行すれば
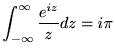
定理 0.3 (Wiener-Khintchineの定理)
証明 0.4
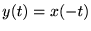 とすると、
とすると、
従って、
ここで、畳み込みの定理より
また、Fourier変換の性質より![$ \mathcal F ^*[x(\tau)]=\mathcal F [x^*(-\tau)]$](img76.png) であるから、
であるから、
離散の場合も同様にして、![$\displaystyle \mathcal F [r_{xx}[n]] = \left\vert X[k]\right\vert^2 $](img81.png) が分かる。
が分かる。
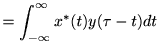 |
||
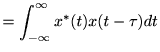 |
従って、
ここで、畳み込みの定理より
また、Fourier変換の性質より
離散の場合も同様にして、
証明終了。